

최근 LeetCode 등의 알고리즘, 구현 문제들을 풀면서 자료 구조를 직접 구현해보기 시작했다.
Heap에 대한 개념은 어느정도 있었다고 생각했는데, 막상 구현하려고 보니 입력, 삭제 시 어떻게 정렬을 보장할 수 있지? 에서 멈칫했다. 생각을 정리하고 코드를 짜보려 했지만, 선뜻 키보드에 손이 가지 않아 정리하는 마음으로 이 포스팅을 작성하게 되었다.
힙(Heap)
힙은 트리 기반의 자료구조이며, 반드시 부모노드와 자식 노드 사이에는 대소 관계가 성립해야한다는 규칙이 있다.
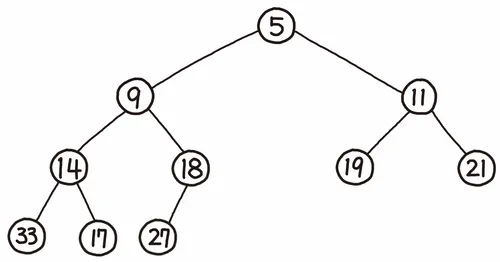
힙에는 규칙에 따라 최소 힙(Min Heap), 최대 힙(Max Heap)이 있으며, 위 대소관계에 따라 부모 노드가 자식 노드보다 작다면 최소 힙, 반대의 경우는 최대 힙이라 부른다. 이 대소 관계는 반드시 부모 노드와 자식 노드 간에만 성립하며, 형제 사이에서는 대소 관계가 정해지지 않는다.
일반적으로 힙이라고 하면, 완전 이진 트리(Complete Binary Tree) 기반의 Binary Heap을 의미한다. 완전 이진 트리란 이진 트리를 만족하면서, 모든 레벨이 왼쪽에서부터 차례대로 채워진 트리 구조를 말한다. 자식이 세 개 이상인 D-ary Heap이나, 비정형 트리를 사용하는 Fibonacci Heap 등 다양한 힙이 있지만, 이 포스팅에서는 일반적인 힙을 다룬다.
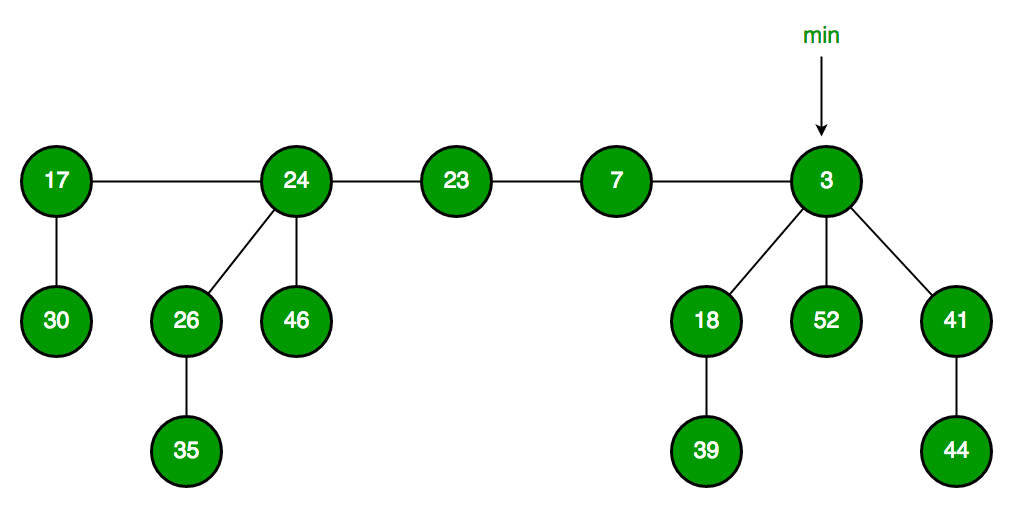
다시 돌아와서, 힙은 데이터를 꺼낼 때 항상 루트 노드에서 데이터를 꺼내는 방식으로 동작한다. 위의 특징들과 더해 유추해보면 최소값 최대값을 조회하는 데 O(1)의 시간이 걸린다. 그래서 주로 최소값이나 최대값을 빠르게 얻기 위해 사용된다. 선형 구조에서는 최소값 최대값을 얻기 위해 기본적으로 O(N)의 시간이 필요하다. 최적화된 탐색 알고리즘을 사용하더라도 O(logN)이다.
이러한 특징을 바탕으로 힙은 실제로 다양하게 활용된다.
- OS 스케줄러의 우선순위 태스크 처리를 위한 최대 힙
- 다익스트라 알고리즘을 활용한 최단거리(최소값)을 구하기 위한 최소 힙
- NodeJS의 이벤트 루프의 Timer Phase - libuv의 타이머 큐(uv_timer)
구현하기 전 마지막으로 알아야할 것이 있다. 위에서 언급한 일반적인 힙인 Binary Heap은 이진 트리 구조임에도 불구하고 배열로 구현할 수가 있다. 자식 노드들의 인덱스나 부모 노드의 인덱스를 구하는 명확한 규칙이 존재하기 때문이다. 이해가 쉽게 그림으로 표현해보았다. 아래 그림은, 배열을 트리 형태의 그림으로 표현한 것이기 때문에 size가 아니라 index임을 알아두자.

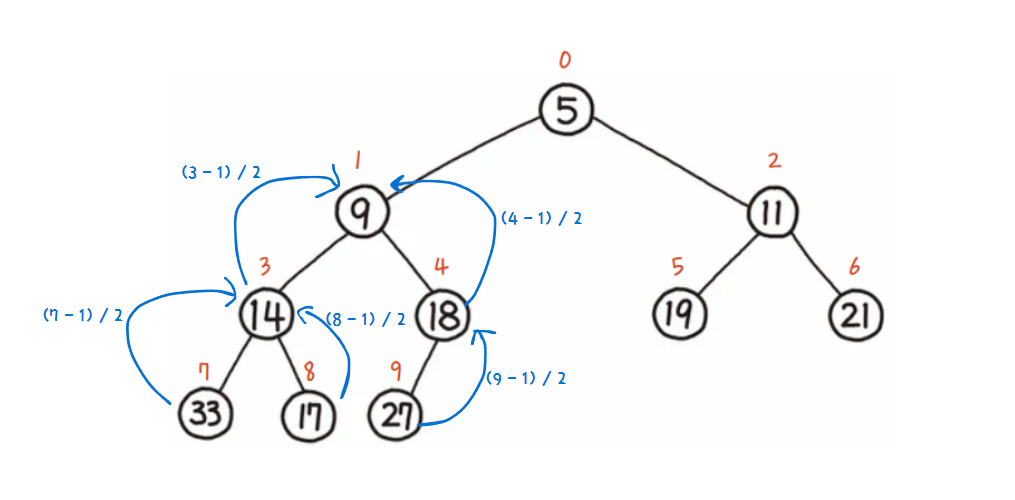
우리는 위 그림에서, 다음과 같은 규칙을 유추할 수 있다. 아래의 규칙을 인지하고 힙을 구현해보자.
왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 * 2 + 1
오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 * 2 + 2
부모 노드 인덱스 = (자식 노드 인덱스 - 1) / 2
구현하기
1. 기본 구조
위에서 언급한 것 처럼, 배열을 사용한 트리 형태의 기본적인 구조를 만들었다. 기본적인 메서드들과 함께 힙 정렬 과정에서 자주 사용되는 요소 교환 함수를 swap이라는 이름으로 구현했다.
type Comparator<T> = (a: T, b: T) => number;
export class Heap<T> {
protected heap: T[] = [];
private comparator: Comparator<T>;
constructor(comparator: Comparator<T>) {
this.comparator = comparator;
}
isEmpty(): boolean {
return this.heap.length === 0;
}
clear(): void {
this.heap = [];
}
peek(): T | null {
return this.isEmpty() ? null : this.heap[0];
}
private swap(i: number, j: number): void {
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
}
}
여기서 Comparator 콜백을 필드로 사용한 이유는, Java의 Comparator 인터페이스에서 영감을 받아, 나중에 PriorityQueue를 구현할 때에 선택적으로 우선순위 정렬을 변경하기 위함이다. 선언 시에 선택적으로 결정할 수 있기 때문에 조금 더 활용하기 용이하다고 생각했다.
// Java
PriorityQueue<Integer> pq = new PriorityQueue<Integer>();
PriorityQueue<Integer> pq = new PriorityQueue<Integer>(Collections.reverseOrder());// TS
const minHeap = new Heap<number>((a, b) => a - b);
const maxHeap = new Heap<number>((a, b) => b - a);
class PriorityQueue<T> extends Heap<T> {}
const pq = new PriorityQueue<number>((a, b) => a - b);
2. 삽입과 삭제
기본적인 insert와 remove를 구현했다. remove에서 T | null을 반환하는 것은 Stack이나 Queue의 pop, poll에서 착안했다.
insert(value: T): void {
this.heap.push(value);
this.heapifyUp();
}
remove(): T | null {
if (this.isEmpty()) {
return null;
}
this.swap(0, this.heap.length - 1);
const removedValue = this.heap.pop()!;
this.heapifyDown();
return removedValue;
}
insert와 remove를 구현할 때, heapify라는 함수를 사용한다. heapify을 직역하면 heap 형태로 바꾸겠다 라는 의미이다. 즉 삽입과 삭제에서 heap처럼 정렬하겠다는 의미라고 이해하면 된다. 재정렬을 위해 삽입 시에는 위로(Up), 삭제 시에는 아래(Down)으로 바라보며 정렬을 수행하게 된다.
remove에서 swap을 먼저 호출하는 이유는, 배열의 pop이 항상 마지막 요소를 삭제하기 때문이다. 위에서 언급한 것 처럼 힙에서 데이터를 꺼낼 때는 항상 루트 노드를 꺼내야하기 때문에, 먼저 swap을 수행한 후 pop으로 루트를 제거하는 방식을 사용한다. 이후 변경된 루트를 기준으로 heapify를 수행한다.
3. Heapify
private heapifyUp(): void {
let index = this.heap.length - 1;
while (
Math.floor((index - 1) / 2) >= 0 && // 부모 노드가 존재할 때
this.comparator(
this.heap[Math.floor((index - 1) / 2)],
this.heap[index]
) > 0 // 부모 노드가 현재 노드보다 우선 순위가 낮을 경우
) {
this.swap(Math.floor((index - 1) / 2), index); // 부모와 교환하며
index = Math.floor((index - 1) / 2); // 인덱스를 부모로 갱신함
}
}
private heapifyDown(): void {
let index = 0;
// 왼쪽 자식 노드가 존재하는 동안 (완전 이진 트리의 특성 상 왼쪽이 먼저)
while (index * 2 + 1 < this.heap.length) {
let smallerChildIndex = index * 2 + 1;
// 오른쪽 자식도 존재하고 오른쪽이 더 우선순위가 높다면
if (
index * 2 + 2 < this.heap.length &&
this.comparator(this.heap[index * 2 + 2], this.heap[index * 2 + 1]) < 0
) {
smallerChildIndex = index * 2 + 2; // 오른쪽 자식을 선택하고
}
// 현재 노드가 자식 노드보다 우선순위가 높다면 중단함
if (this.comparator(this.heap[index], this.heap[smallerChildIndex]) < 0) {
break;
}
this.swap(index, smallerChildIndex); // 자식과 교환하며
index = smallerChildIndex; // 다음 탐색 위치로 갱신함
}
}
insert에서 사용하는 heapify는 마지막 index에 삽입되기 때문에, 상향식을 통해 부모 노드와 계속 우선순위를 비교하여 정렬을 수행한다. 반대로 remove는 하향식을 통해 제거된 루트 노드의 위치에서부터 자식 노드와 계속 비교하며 정렬을 수행하게 된다. 즉, 삽입은 자식이 부모를 향해 올라가며 정렬하고, 삭제는 부모가 자식을 향해 내려가며 정렬하는 형태이다.
(완성된 heap의 전체 코드는 깃허브에서 볼 수 있다)
4. 테스트해보기
테스트에 사용된 input은 위 그림의 heap 숫자를 그대로 사용했다.
describe("heap", () => {
describe("minHeap", () => {
it("heapify up when inserting a value", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const minHeap = new Heap<number>((a, b) => a - b);
input.forEach((v) => minHeap.insert(v));
const expected = [...input].sort((a, b) => a - b);
expect(minHeap.peek()).toBe(Math.min(...input));
const result: number[] = [];
while (!minHeap.isEmpty()) {
result.push(minHeap.remove()!);
}
expect(result).toEqual(expected);
});
it("heapify down when removing a value", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const minHeap = new Heap<number>((a, b) => a - b);
input.forEach((v) => minHeap.insert(v));
const removeLength = input.length / 2;
for (let i = 0; i < removeLength; i++) {
minHeap.remove();
}
const expected = [...input]
.sort((a, b) => a - b)
.slice(removeLength, input.length);
const result: number[] = [];
while (!minHeap.isEmpty()) {
result.push(minHeap.remove()!);
}
expect(result).toEqual(expected);
});
});
describe("maxHeap", () => {
it("heapify up when inserting a value", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const maxHeap = new Heap<number>((a, b) => b - a);
input.forEach((v) => maxHeap.insert(v));
const expected = [...input].sort((a, b) => b - a);
expect(maxHeap.peek()).toBe(Math.max(...input));
const result: number[] = [];
while (!maxHeap.isEmpty()) {
result.push(maxHeap.remove()!);
}
expect(result).toEqual(expected);
});
it("heapify down when removing a value", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const maxHeap = new Heap<number>((a, b) => b - a);
input.forEach((v) => maxHeap.insert(v));
const removeLength = input.length / 2;
for (let i = 0; i < removeLength; i++) {
maxHeap.remove();
}
const expected = [...input]
.sort((a, b) => b - a)
.slice(removeLength, input.length);
const result: number[] = [];
while (!maxHeap.isEmpty()) {
result.push(maxHeap.remove()!);
}
expect(result).toEqual(expected);
});
});
});
우선순위 큐(Priority Queue)
이미 Heap을 구현해뒀기 때문에 우선순위 큐는 기존의 Heap을 확장만 해주면 된다.
export class PriorityQueue<T> extends Heap<T> {
constructor(comparator: (a: T, b: T) => number) {
super(comparator);
}
enqueue(item: T): void {
this.insert(item);
}
dequeue(): T | null {
return this.remove();
}
}
describe("priorityQueue", () => {
it("enque elements in priority order", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const priorityQueue = new Heap<number>((a, b) => a - b);
input.forEach((v) => priorityQueue.insert(v));
const expected = [...input].sort((a, b) => a - b);
expect(priorityQueue.peek()).toBe(Math.min(...input));
const result: number[] = [];
while (!priorityQueue.isEmpty()) {
result.push(priorityQueue.remove()!);
}
expect(result).toEqual(expected);
});
it("dequeue elements in priority order", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const priorityQueue = new Heap<number>((a, b) => a - b);
input.forEach((v) => priorityQueue.insert(v));
const removeLength = input.length / 2;
for (let i = 0; i < removeLength; i++) {
priorityQueue.remove();
}
const expected = [...input]
.sort((a, b) => a - b)
.slice(removeLength, input.length);
const result: number[] = [];
while (!priorityQueue.isEmpty()) {
result.push(priorityQueue.remove()!);
}
expect(result).toEqual(expected);
});
it("enque elements in rerverse priority order", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const priorityQueue = new Heap<number>((a, b) => b - a);
input.forEach((v) => priorityQueue.insert(v));
const expected = [...input].sort((a, b) => b - a);
expect(priorityQueue.peek()).toBe(Math.max(...input));
const result: number[] = [];
while (!priorityQueue.isEmpty()) {
result.push(priorityQueue.remove()!);
}
expect(result).toEqual(expected);
});
it("dequeue elements in reverse priority order", () => {
const input = [33, 17, 27, 14, 5, 9, 19, 21, 18, 11];
const priorityQueue = new Heap<number>((a, b) => b - a);
input.forEach((v) => priorityQueue.insert(v));
const removeLength = input.length / 2;
for (let i = 0; i < removeLength; i++) {
priorityQueue.remove();
}
const expected = [...input]
.sort((a, b) => b - a)
.slice(removeLength, input.length);
const result: number[] = [];
while (!priorityQueue.isEmpty()) {
result.push(priorityQueue.remove()!);
}
expect(result).toEqual(expected);
});
});
참조.
https://www.youtube.com/watch?v=AjFlp951nz0
https://github.com/libuv/libuv/
https://www.geeksforgeeks.org/types-of-heap-data-structure/#6-dary-heap
https://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)

diehreo@gmail.com
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] 해시테이블 (hashtable)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbyW8af%2FbtshjcKvJyq%2FaKfoQQFyz1p4hJI5zFlOVK%2Fimg.png)
![[자료구조] 트리(Tree) 구조](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FR5CeZ%2FbtrWxquyvdF%2FHbqtdQKSXwHEOMhQR4I8uk%2Fimg.webp)