[알고리즘] LIS (Longest Increasing Subsequence)

LIS(최장 증가 부분 수열)

N크기의 배열이 주어졌을때, 배열에서 일부 원소를 조합하여 만든 부분 수열 중, 오름차순의 조건을 만족하면서 길이가 최대인 부분 수열을 말한다.

 

아래처럼, {3, 6, 2, 1, 7, 8, 5, 4, 9}의 배열이 있다면, LIS는 {3, 6, 7, 8, 9} 이다

 

 

DP

LIS 문제는 각 요소를 포함하는 증가하는 부분 수열의 최대 길이를 찾는 문제로 이를 효율적으로 해결하기 위해 동적 계획법을 사용한다.

단일 배열 내에서, 이전 인덱스의 숫자와 비교하여 증가시켜주면 되기 때문에 DP로 문제를 해결할 수 있다.

단일 배열이라는 점만 제외하면 LCS와 유사한 매커니즘이기에, 점화식도 비슷한 방법으로 구현할 수 있다.

 

 

[알고리즘] LCS (Longest Common Subsequence, Longest Common Substring)

 

 

점화식

for (int i = 0; i < N; i ++) {
    dp[i] = 1;

    for(int j = 0; j < i; j ++) {
        if (line[i][1] > line[j][1]) {
            dp[i] = Math.max(dp[j] + 1, dp[i]);
        }
    }
}

 

위의 코드를 실행하면 dp배열이 각 요소를 포함하는 최장 증가 부분 수열의 길이를 저장하게 되며, 이를통해 최종 LIS를 구할 수 있다.

 

 

 

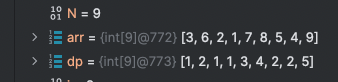
점화식에서 알 수 있듯이, 시간 복잡도는 O(N^2)로,  시간복잡도를 고려해야하는 문제에서는 시간 초과가 발생할 수 있다.

(해당 문제는 백준의 전깃줄-2 이다.)

 

 

 

---

 

 

이진 탐색

LIS를 구할 때, O(N logN)의 시간 복잡도를 가진 이진 탐색으로 구할 수 있다.

LIS는 단일 시퀀스 내에서 증가하는 부분 수열을 찾는 문제이기 때문에 이진 탐색으로 해결할 수 있지만
LCS는 두 시퀀스 간의(=두 문자열의 공통부분) 공통 부분을 찾는다. 두 시퀀스를 모두 비교해야하기 때문에 이진 탐색으로는 효율적으로 해결이 불가능하다.

 

 

기본적인 이진 탐색은, 정렬된 배열에서 특정한 값이 배열 내에 어디에 위치하는지를 계속 반으로 나눠서 위치를 특정할 수 있다.

 

[알고리즘] 이진탐색(이분탐색) - Binary Search

 

 

LIS에서의 이진 탐색은, 정렬된 배열을 사용하지 않고, LIS를 유지하면서 각 요소의 삽입 위치를 이진 탐색을 통해 업데이트한다.

 

List<Integer> lis = new ArrayList<Intger>;
for (int i = 0; i < N; i++) {
	binarySearch(lis, arr[i]);
}

private static void binarySearch(List<Integer> lis, int current) {
    int start = 0;
    int end = lis.size();

    //current가 들어갈 위치를 찾는다.
    while(start < end) {
        int mid = (start + end) / 2;
        if (lis.get(mid) >= current) {
            end = mid;
        }
        else start = mid + 1;
    }

    //업데이트
    if (start >= lis.size()) lis.add(current);
    else lis.set(start, current);
}

 

 

하지만 이를 출력해보면 {1, 4, 7, 8, 9}를 얻을 수 있는데 이는, 아래와 같은 동작을 거쳐 해당 원소들의 위치를 찾아 강제로 변경하기 때문이다.

 

 

 

 

해당 원소들의 실제 인덱스를 알아야겠구나!!!! 라고 생각이 들었다면, 바로 구현해보자.

 

실제 인덱스를 알아야 하는 이유는 위의 경우처럼 리스트에는 최장 부분 수열의 길이만 확정적으로 알 수 있고
{1, 4, 7, 8, 9}와 같이 전혀 다른 (LIS가 아닌) 부분 수열이 올 수도 있기 때문이다.

 

 

//arr의 인덱스의 숫자들이 들어가는 위치를 저장
int[] realIdx = new int[N];

List<Integer> lis = new ArrayList<>();
for (int i = 0; i < N; i++) {
	realIdx[i] = binarySearch(lis, arr[i]);
}

private static int binarySearch(List<Integer> lis, int current) {
    int start = 0;
    int end = lis.size();

    //current가 들어갈 위치를 찾는다.
    while(start < end) {
        int mid = (start + end) / 2;
        if (lis.get(mid) >= current) {
            end = mid;
        }
        else start = mid + 1;
    }

    //업데이트
    if (start >= lis.size()) lis.add(current);
    else lis.set(start, current);
    
    return start;
}

 

 

 

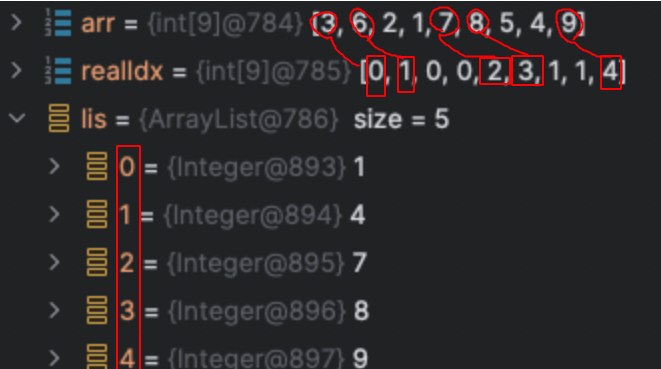
이제 리스트와, idx배열을 역순 추척하여 해당 요소가 LIS의 일부인지 확인하고, 해당 요소를 리스트에서 제거하는 방식으로 추적할 수 있다. LIS의 각 요소는 이전 요소보다 커야하기 때문에, 역순 추적을 하면 올바른 순서로 추적할 수 있다.

 

StringBuilder sb = new StringBuilder();

int lisLen = lis.size();
for (int i = N - 1, l = lisLen - 1; i >= 0 && l >= 0; i--) {
    if (realIdx[i] == l) {
        sb.append(arr[i] + " ");
        l--;
    }
}

System.out.println(sb.reverse().toString().trim());
//3 6 7 8 9

 

 

 

 

---

 

참조

Longest Increasing Subsequence (LIS) - GeeksforGeeks

알고리즘 - 최장 증가 부분 수열(LIS) 알고리즘