![[알고리즘] 벨만-포드(Bellman-Ford) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbV3s2z%2FbtsH6L7RYjN%2Fqv6Ik1UXxZbtfbkaISb25k%2Fimg.png)

벨만-포드 알고리즘은 그래프의 최단 경로를 구하는 알고리즘의 하나로, 다익스트라로 해결하지 못하는 음의 간선이 포함된 문제를 효과적으로 해결할 수 있는 알고리즘이다.
[알고리즘] 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘그래프의 최단 경로를 구하는 알고리즘으로 하나의 정점에서 출발하여 최단 거리를 구하는 알고리즘이다. 탐욕법(Greedy)과 동적 계획법을 사용하는 알고리즘으로,
mag1c.tistory.com
다익스트라 vs 벨만-포드
백준 웜홀 문제의 2번 예시로 그래프를 그려보았다.

우리가 눈으로 보았을 때, 실제 1에서 1까지의 최단경로는 0이 아니라 한 바퀴를 돌았을 때, 무한히 -2의 가중치를 계속해서 더하는 경로이다. 1에서 3의 최단경로 또한 1에서 3까지의 최단경로는 0이지만, 1에서 1까지의 최단경로가 무한한 음의 가중치를 가지기 때문에 3또한 영향을 받아 무한히 감소하는 음수 사이클을 가지게 된다. 이는 곧 음의 무한대를 의미하며 코드 실행 시 무한히 동작할 것 같은 기대(?)를 갖게 한다.
실제로 다익스트라를 구현하여 이 문제를 해결하려고 하면 어떻게 될까?
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
private static class Node implements Comparable<Node> {
int node; int cost;
private Node(int node, int cost) {
this.node = node;
this.cost = cost;
}
@Override
public int compareTo(Node o) {
return cost - o.cost;
}
}
private static ArrayList<ArrayList<Node>> nodeList = new ArrayList<>();
private static int[] dist;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
for (int i = 0; i <= N; i ++) {
nodeList.add(new ArrayList<>());
}
for (int i = 0; i < M; i ++) {
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
nodeList.get(A).add(new Node(B, C));
}
for (int i = 1; i < nodeList.size(); i ++) {
for (Node node: nodeList.get(i)) {
System.out.println(i + " → " + node.node + "(거리 : " + node.cost + ")");
}
}
dist = new int[N + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
dijkstra(1);
for (int i = 1; i <= N; i ++) {
System.out.println("1에서 " + i + "까지의 거리 : " + dist[i]);
}
}
private static void dijkstra(int start) {
PriorityQueue<Node> q = new PriorityQueue<>();
q.offer(new Node(start, 0));
dist[start] = 0;
while(!q.isEmpty()) {
Node cur = q.poll();
System.out.println("현재 노드: " + cur.node + ", 가중치: " + cur.cost);
for (Node node: nodeList.get(start)) {
if (dist[node.node] > dist[cur.node] + node.cost) {
dist[node.node] = dist[cur.node] + node.cost;
q.offer(new Node(node.node, node.cost));
System.out.println("노드 " + node.node + "까지의 가중치 갱신(가중치: " + dist[node.node] + " )");
}
}
}
}
}
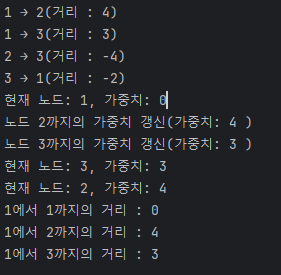
실행이 끝나지 않고 계속 무한사이클을 돌 줄 알았지만, 1에서 1까지의 거리는 0, 1에서 3까지는 3이라는 결과를 보여주었다.
이처럼, 최단 경로가 무한히 줄어들 때, 다익스트라 알고리즘으로는 원하는 문제를 해결할 수 없다. 애초에 최단거리를 찾을 수 없기 때문이다. 또한 위의 코드 결과에서 알 수 있듯이 다익스트라 알고리즘으로는 도출된 답이 틀렸는지, 맞았는지 알 수도 없다.
벨만-포드
벨만-포드 알고리즘은 다익스트라 알고리즘 처럼 최단 경로를 구하는 데 사용되지만, 음의 가중치가 있는 간선이 포함된 그래프에서도 올바르게 동작하는 것을 보장할 수 있다.
음수 사이클을 감지하여 최단 경로가 무한히 줄어드는 경우를 알 수 있기 때문에, 음의 가중치가 있는 경우에는 벨만-포드 알고리즘을 사용하는 것이 적합하다.
벨만-포드 알고리즘의 구현 과정은 N - 1번의 릴렉세이션을 수행한 후, 한번 더 릴렉세이션을 수행하여 음의 가중치가 있는지 확인한다. N - 1번의 릴렉세이션을 수행하는 이유는, 최단 경로가 최대 N - 1개의 간선을 가질 수 있기 때문이다. 모든 간선을 통과하는 경우가 최단 경로일 경우가 존재할 수 있다는 의미이다.
릴렉세이션(Relaxation)
간선을 통해 더 짧은 경로를 발견하면 해당 경로로 거리를 업데이트 하는 과정.
벨만-포드 알고리즘은 다익스트라 알고리즘과 달리, 모든 간선을 우선적으로 사용하지 않아도 된다. N - 1번 모든 노드를 거쳐 탐색하기 때문에 간선을 반복적으로 릴렉세이션하지 않아도 된다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private static class Edge {
int from, to, cost;
private Edge(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
}
private static ArrayList<Edge> edgeList = new ArrayList<>();
private static int[] dist;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
edgeList.add(new Edge(A, B, C));
}
for (Edge edge: edgeList) {
System.out.println(edge.from + " → " + edge.to + "(거리 : " + edge.cost + ")");
}
dist = new int[N + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
boolean hasNegativeCycle = bellmanFord(1, N);
if (hasNegativeCycle) {
System.out.println("음수 사이클 존재");
} else {
for (int i = 1; i <= N; i++) {
System.out.println("1에서 " + i + "까지의 거리 : " + (dist[i] == Integer.MAX_VALUE ? "INF" : dist[i]));
}
}
}
private static boolean bellmanFord(int start, int N) {
dist[start] = 0;
// N-1번의 릴렉세이션(relaxation) 수행
for (int i = 1; i < N; i++) {
for (Edge edge: edgeList) {
if (dist[edge.from] != Integer.MAX_VALUE && dist[edge.to] > dist[edge.from] + edge.cost) {
dist[edge.to] = dist[edge.from] + edge.cost;
}
}
}
// 추가 릴렉세이션으로 음수 사이클 검증
for (Edge edge: edgeList) {
if (dist[edge.from] != Integer.MAX_VALUE && dist[edge.to] > dist[edge.from] + edge.cost) {
return true; // 음수 사이클 존재
}
}
return false; // 음수 사이클 존재하지 않음
}
}

관련 문제
해당 문제를 풀어보면, 벨만-포드 알고리즘 구현의 기초를 다질 수 있을 것 같다.

diehreo@gmail.com
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[알고리즘] LIS (Longest Increasing Subsequence)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FsCe9Y%2FbtsH65ruDd8%2F2S7xZnsiVBXmfzqVviFg9K%2Fimg.png)
![[알고리즘] 다익스트라(Dijkstra) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcQgVSa%2FbtsH6xorwBZ%2FCZXQvj5Ittl2DFhR1T6ATk%2Fimg.png)