Dynamic Programing
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다. - 위키백과
Dynamic Programing은
1. 하위 문제로 쪼개지며, 하위 문제의 정답으로 해당 문제의 정답을 구할 수 있을 때(Optimal Substructure)
2. 하위 문제가 겹칠 때 (Overlapping Subproblem)
사용할 수 있다.
Top-Bottom방식과 Bottom-Up방식이 있는데
이름에서 알 수 있다시피 위에서아래로, 아래에서 위로 가는 방식인 것 같다.
Top-Bottom은 재귀를 통해 메인 문제에서 작은 문제들로 쪼개어가는 과정이고
Bottom-Up방식은 반복문을 통해 쪼개어진 최하단의 문제들로부터 메인 문제를 풀어가는 과정이라고 이해했다.
(개인적 생각)
DP는 문제를 정의하고, 해당 문제에 따른 하위 문제를 정의하는 것만 잘할 수 있으면 될 것 같다.
예제 - 피보나치 수열 구하기
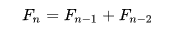

피보나치 수열 7번째의 값을 구하는 과정이다.
위에 적어놓은 대로, 사용할 수 있는지 판단해보자.
1. F(7)을 구하기 위해 하위 문제인 F(6), F(5)..........로 나눌 수 있다.
2. 하위 문제의 결과들로 F(7)을 구하기 위한 F(6)과 F(5)의 값을 알 수 있고, 메인 문제인 F(7)의 결과를 알 수 있다.
3. 하위 문제들이 겹치고 있다.
코드로 작성해보자.
public int fibo(int n) {
if(n==0) return 0;
if(n==1) return 1;
return fibo(n-1) + fibo(n-2);
}
위의 방법처럼 재귀적으로 시도할 경우 구하는 수가 커질 경우 call stack이 overflow가 될 수 있다.
F(10000)을 구한다고 가정해보자.
현재 알고있는 값은 0번째와, 1번째의 값 뿐이기 때문에, 결국 F(1)까지 호출이 되어 순차적으로 해를 구할 수 있는데, 이렇게 되면 stack에 F(10000), F(9999), F(9998) ............... F(1)까지 채워지게되고, 결국 limit을 초과하여 StackOverFlowError가 발생하게 된다.
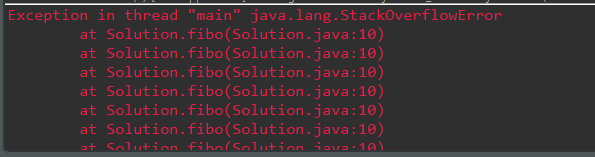
기존 문제는 상위 문제에서 하위 문제로 쪼개어 나가는 방식이었기 때문에 발생했다.
위의 방식을 Top-Down 방식이라고 하며, Top-Down 방식은 재귀적으로 풀어 나간다.
이를 해결하기 위해, Bottom-Up 방식의 DP를 적용할 수 있다.
Bottom-Up 방식이란 가장 작은 하위 문제부터 해결해 나가는 방식이다.
Bottom-Up 방식은 재귀적으로 해결하는 것이 아닌, 반복문을 사용하여 하위 문제부터 해결해 나간다.
Bottom-Up 방식의 피보나치 수열을 구하는 코드를 작성해보았다.
static List<Integer> list = new ArrayList<Integer>() {{
add(0);
add(1);
}};
public int fibo2(int n) {
if(n==0) return 0;
if(n==1) return 1;
for(int i=2; i<n+1; i++) {
int num = list.get(i-1) + list.get(i-2);
list.add(num);
}
return list.get(n);
}하위 문제들 부터 풀어나가며, List에 추가한 후, n번째 수를 구하는 코드이다.
또한, Top-Down에서는 구하지 못했던 F(10000)의 값도 구할 수 있다.
이러한 Bottom-Up방식의 시간복잡도는 O(n)이고, 공간복잡도는 O(n)이지만
공간복잡도는 해당 피보나치 수열을 구하기 위한 F(n-1), F(n-2)만을 필요로 하기 때문에, O(1)까지 줄일 수 있다.
import java.util.ArrayList;
import java.util.List;
class Solution{
static List<Integer> list = new ArrayList<Integer>() {{
add(0);
add(1);
}};
public int fibo(int n) {
if(n==0) return 0;
if(n==1) return 1;
return fibo(n-1) + fibo(n-2);
}
public int fibo2(int n) {
if(n==0) return 0;
if(n==1) return 1;
for(int i=2; i<n+1; i++) {
int num = list.get(i-1) + list.get(i-2);
list.add(num);
}
return list.get(n);
}
public static void main(String[] args) {
long startTime = System.nanoTime();
Solution sol = new Solution();
System.out.println(sol.fibo(40));
long endTime = System.nanoTime();
long durationTimeSec = endTime - startTime;
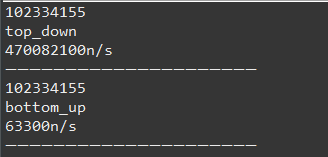
System.out.println("top_down");
System.out.println(durationTimeSec + "n/s");
System.out.println("ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ");
/*********************************************/
long startTime2 = System.nanoTime();
Solution sol2 = new Solution();
System.out.println(sol2.fibo2(40));
long endTime2 = System.nanoTime();
long durationTimeSec2 = endTime2 - startTime2;
System.out.println("bottom_up");
System.out.println(durationTimeSec2 + "n/s");
System.out.println("ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ");
}
}